Introdução à Criptografia – Parte 2

Na primeira parte desta série eu falei bastante sobre alguns fundamentos da criptografia e principalmente sobre a criptografia reversível de chave simétrica. Vimos que um problema crônico existente com os algoritmos simétricos e que atormentou os cientistas durante muito tempo era como poderia ocorrer de forma segura a troca das chaves, para que as partes A e B pudessem se comunicar de maneira criptografada.

Se tiver a oportunidade de me encontrar pessoalmente com a outra parte, ok, podemos conversar de forma reservada e lhe conto a chave que será usada. Mas e se ele estiver distante, sem a possibilidade de um encontro pessoal, o que exigirá o envio da chave via meio digital, posso enviar via email ou WhatsApp? Claro que não!

Este problema atormentou muita gente. Na Segunda Guerra Mundial o livro dos códigos da Enigma (a máquina de criptografia das mensagens alemãs), com chaves diárias de um mês inteiro, era entregue em mãos aos operadores de rádio. Este tinha ordens para, sob ataque, imediatamente destruir a máquina e o livro. Se os aliados tivessem acesso a este livro seriam capazes de quebrar as comunicações de um mês inteiro (e isso inclusive aconteceu, através de suborno a um agente alemão, mas essa história fica pra outro dia).

Seria possível a troca de chaves de forma segura usando um meio de comunicação inseguro como a Internet? Durante muito tempo não foi, até a chegada de Diffie e Hellman.

O algoritmo Diffie-Hellman

A troca segura de chaves criptográficas por meio inseguro se consagrou como matematicamente impossível durante muito tempo, exceto para os pesquisadores Martin Hellman e Whitfield Diffie. Eles pensaram em um protocolo de troca de informações sigilosas via correio que é interessante para ilustrar como isso levaria mais tarde a um dos algoritmos de segurança mais famosos e importantes do mundo. Este exemplo foi me ensinado por meu professor de segurança da informação durante a faculdade, Elgio Schlemer:

Imagine que quero enviar documentos sigilosos pelo correio para “P” e que eu não confio no carteiro. Colocar os documentos em uma caixa com cadeado não serve, pois como enviaria a chave do cadeado para o “P”? Se não confio no meio, não adianta variar os métodos usando este meio de transporte no qual não confio. Mas Diffie e Hellman pensaram em um método (eu sou o “E” enviando documentos para “P”):

“E” compra um cadeado em uma ferragem;
“E” coloca os documentos em uma caixa e coloca o seu cadeado. Pressupõe-se que tanto a caixa como o cadeado são invioláveis e que a única forma de abrir a caixa é com a chave;
“E” envia a caixa pelo Correio. Veja que ninguém poderá abir, pois “E” não enviou a chave. O carteiro curioso nada pode fazer;
“P” recebe a caixa. Bom, “P” também não a pode abrir pois ele não tem a chave (surpreso?). Mas “P” ao invés de abrir, compra o seu cadeado e coloca ele também na caixa. A caixa agora tem DOIS cadeados: o de “E” e o de “P”;
“P” devolve a caixa pelo correios ao “E”;
Legal, agora nem mesmo “E” consegue abrir sua caixa. Mas ele apenas usa a sua chave para tirar o seu cadeado, mantendo o cadeado de “P”;
“E” devolve a caixa para “P” que agora pode abrí-la.

Observe que neste protocolo jamais houve uma troca de chaves. Diffie e Hellman pensavam que deveria existir um princípio matemático que reproduzisse este efeito e depois de muita pesquisa o encontraram na aritmética modular usando números primos. O famoso e ainda extremamente usado algoritmo RSA é baseado na mesma aritmética modular do Diffie-Hellman, embora ele em sua forma original somente seja usado para fins acadêmicos.

Criptografia Assimétrica

Um algoritmo e criptografia assimétrico ou criptografia de chave assimétrica, portanto, é quando se usa uma chave para cifrar, porém, magicamente, esta chave não serve para decifrar o que se cifrou. Muitos chamam estes algoritmos de “chave pública e privada”, mas o nome técnico deles é algoritmos assimétricos. Esta confusão no nome é porque uma das chaves, normalmente a que serve para cifrar, é tornada pública e a outra é mantida sob sigilo conhecida como chave privada.

Para entendermos um algoritmo assimétrico voltemos aos correios e ao uso das caixas. Tem uma maneira ainda mais eficiente de receber ou enviar documentos sigilosos.

Digamos que eu quero enviar um documento para “P”. Bastaria isto:

“P” compra um cadeado e me envia ele ABERTO pelo correio. Não envia a chave;
“E” recebe o cadeado aberto de “P” e o usa para fechar a caixa. Uma vez fechada, “E” já não tem mais condições de abrí-la;
“E” envia a caixa com o cadeado fechado de “P”;
“P” a abre pois tem a chave.

Nesta analogia a chave pública seria o cadeado aberto: ele só serve para cifrar.

Estendendo a analogia, “P” poderia pedir a um fabricante de cadeados que confeccionasse milhares de cadeados com a mesma chave. O cadeado de “P” estaria em todas as agências de correios, por exemplo. Esta é a ideia.

Claro que para que isto funcione o cadeado deve ser forte e a chave deve possuir muitas combinações, senão um ataque de força bruta seria viável. Deve também ser imune a criptoanálise, ou seja, nenhum chaveiro do mundo seria capaz de construir uma nova chave apenas analisando o cadeado.

Voltando aos termos “técnicos” a ideia do cadeado foi implementada pelo algoritmo RSA baseado na fatoração de números primos. Constitui em duas chaves, uma chamada de Ke (K para “e”ncriptar) e Kd (k para “d”ecriptar). Uma complementa a outra. O que cifra-se usando Ke apenas com a Kd é possível recuperar.

Um atacante conhece Ke pois a tornei pública. Contudo, mesmo tendo ela, ele está computacionalmente inviabilizado de calcular Kd. RSA garante isto através do uso de números primos gigantes, em 2009 (quando estudava criptografia na faculdade) usávamos 512 bits, atualmente, 2048!!! Isso por causa do aumento e capacidade computacional a que temos acesso.

Para que esta troca de chaves funcione com o algoritmo Diffie-Hellman, deve-se escolher chaves que sejam fortes o bastante para não serem descobertas por força bruta e que a operação realizada com elas seja comutativa, como a multiplicação, a soma e o XOR (muito comum na criptografia simétrica também).

Aqui segue um exemplo usando números e a operação de multiplicação:

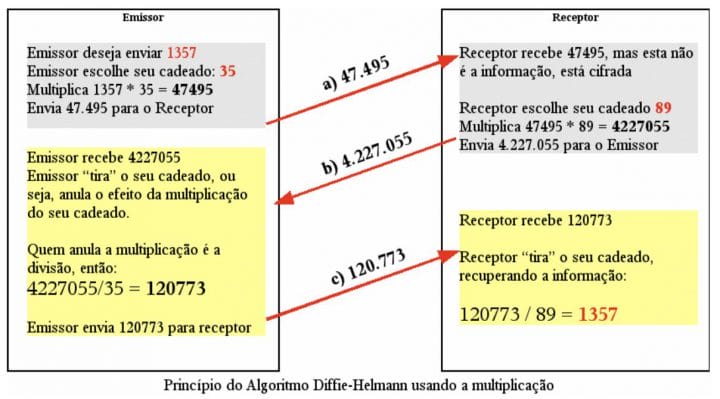
Da forma como ilustrado, nenhuma das informações que está em vermelho (1357, 35, 89) foi transmitida, no entanto o receptor foi capaz de recuperar com sucesso a informação correta.

Considerando que um atacante, observando o tráfego, tenha cópias de todas as mensagens, ele tem os valores da mensagem a (47.495), da mensagem b (4.227.055) e da mensagem c (120.773), mas não tem a chave.

O que torna a multiplicação inviável é justamente porque o atacante tem como descobrir estes valores apenas com as mensagens que obteve. Se o atacante dividir b por a, terá o cadeado do receptor (4227055/47495=89). Óbvio! Se ele dividir b por c terá o cadeado do Emissor. Pronto. Não serve. Era necessário não apenas um princípio matemático que tivesse as propriedades citadas, mas que também fosse irreversível. Multiplicação não serve, pois a divisão o reverte.

No caso do Diffie-Hellman, eles usaram as operações de potenciação e de módulo (mod – %) que permitem a comutatividade mas sendo bem eficientes contra a força bruta, usando uma fórmula como a abaixo:

(23 ^ x) mod 1311 = 1127

Onde não temos como calcular rapidamente o valor de x sem ser por força bruta, estando à mercê do tamanho de x. O algoritmo completo pode ser encontrado na imagem abaixo:

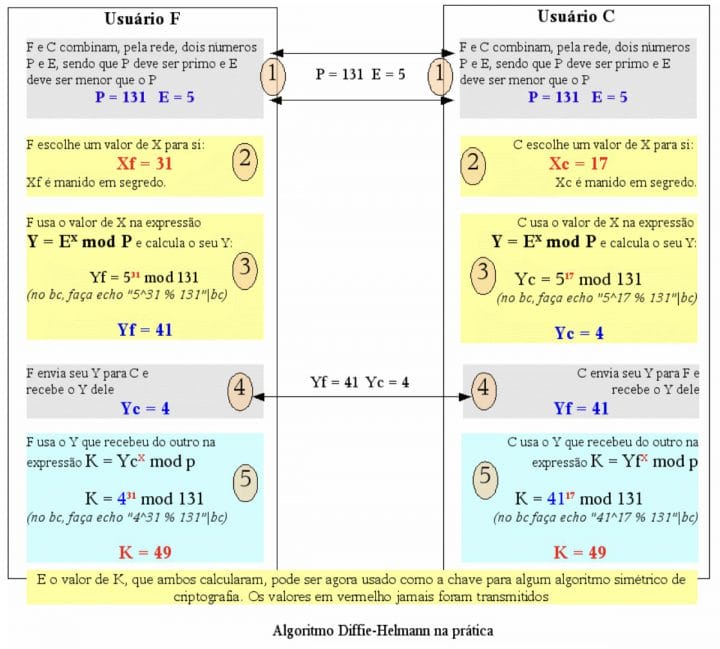
Com números pequenos ainda se é vulnerável ao ataque por força bruta, pois o atacante, não tendo nenhum dos valores de X, poderá tentar usar alguns possíveis valores até acertar. Porém se usar números realmente grandes, da ordem de 2048 bits, o número de tentativas torna inviável este ataque.

RSA

Foram os pesquisadores Ronald Rivest, Adir Shamir e Leonard Adlemann que chegaram ao primeiro algoritmo de cifra assimétrico, o popularmente conhecido algoritmo RSA. O coração do RSA consiste na mesma função de mão única descoberta por Whitfield Diffie e Martin Hellman: a função modular. Novamente, assim como no algoritmo Diffie-Hellman, a segurança está no emprego de números realmente gigantes, hoje da ordem de 2048 bits (eram 512 em 2009!). Devido a esse esforço computacional necessário seu uso foi considerado como não prático durante muitos anos. Seu uso de forma segura requer a escolha de números muito grandes, fazendo com que o resultado, principalmente, seja igualmente de muitos bits, o que facilmente gera números com mais de 100 mil dígitos!!!

Este foi um dos impasses a que chegaram os pesquisadores britânicos e que os fizeram achar o algoritmo impraticável devido ao fato de que os cálculos exigiam muito processamento, muito além do hardware existente na época. Ainda hoje isto é uma completa utopia se não fosse possível simplificar a operação através de reduções matemáticas complexas. Sem este atalho matemático o RSA seria inviável, já com os atalhos matemáticos o RSA pode ser usado, mas ainda assim ele é considerado um algoritmo que consome uma monstruosidade de processamento. Por isso seu emprego deve ser muito, mas muito restrito.

Resumindo, pode-se dizer que os algoritmos assimétricos são extremamente onerosos, ou seja, consomem muita CPU. Seu uso deve ser evitado ou, pelo menos, minimizado pois o processador agradece. Como os simétricos são absolutamente seguros e rápidos, sendo seu único problema a troca de chave, é comum usar um assimétricos apenas para trocar a chave convergindo após para um simétrico. O protocolo SSL é exatamente assim (que está por trás do SSH e o HTTPS, dentre outros).

De forma muito resumida, o que o SSL faz é mais ou menos o seguinte:

Cliente e servidor concordam em qual algoritmo simétrico irão utilizar. Exemplo: AES;
Cliente solicita a chave pública do servidor (na prática chama-se certificado, mas como disse, estou descrevendo de forma muito resumida);
Cliente escolhe aleatoriamente uma chave k de sessão;
Cliente cifra a chave que ele escolheu com a chave pública do servidor;
Cliente envia k cifrado para o servidor. Até aí se usou o algoritmo assimétrico;
Servidor recebe k cifrado, decifra com a sua chave privada;
Cliente e servidor agora conversam usando o AES usando a chave simétrica k.

Esta é a ideia, usar o oneroso algoritmo assimétrico apenas o necessário, nada além disto.

Outras aplicações muito populares usam vários tipos de cifras, cada uma dentro do seu contexto, de forma que os assimétricos não estão aí para substituir os simétricos, mas sim para complementá-los.

Abaixo um exemplo de uso prático do RSA em JavaScript, em uma função que assina um token JWT utilizando o referido algoritmo com uma chave privada. Isso é útil em cenários que um mesmo token deve ser aceito por diferentes aplicações. Com criptografia simétrica, a chave teria de ser compartilhada entre as aplicações o que ;e terrível do ponto de vista de segurança. Mas com RSA eu tenho a chave privada apenas no sistema emissor dos tokens (geralmente armazenada em um arquivo private.key, .pem ou .cert).


import jwt from 'jsonwebtoken';
import fs from 'fs';

const privateKey = fs.readFileSync('private.key', 'utf8');

function sign(accountId) {
    const token: Token = { accountId };
    return jwt.sign(token, privateKey, { expiresIn: parseInt(`${process.env.JWT_EXPIRES}`), algorithm: "RS256" });
}

import jwt from 'jsonwebtoken';

import fs from 'fs';

const privateKey = fs.readFileSync('private.key', 'utf8');

function sign(accountId) {

const token: Token = { accountId };

return jwt.sign(token, privateKey, { expiresIn: parseInt(`${process.env.JWT_EXPIRES}`), algorithm: "RS256" });

}

Já a chave pública (em um arquivo public.key, .pem ou .cert) sim eu posso distribuir sim por todos sistemas, que estarão aptos a verificar com ela se a chamada de um cliente com um token assinado é válida ou não, como no código abaixo.


import jwt from 'jsonwebtoken';
import fs from 'fs';

const publicKey = fs.readFileSync('public.key', 'utf8');

async function verify(token) {
     const decoded = await jwt.verify(token, publicKey, { algorithm: ["RS256"] });
     return { accountId: decoded.accountId, jwt: token };
}